Accelerators for Complex Valued Neural Networks

Complex Valued Neural Networks (CVNNs) stand out for their unique capability to handle complex numbers, acheiving high performances in applications such as radar, MRI, and sonar imaging. Despite their potential, accelerating CVNNs introduce significant challenges, particularly in terms of complex number representation and operation. Our research project focus on a software-hardware co-design to overcome the challenges, specifically leveraging the inherent properties of complex numbers and the unique characteristics of CVNNs.

Understanding Complex Valued Neural Networks

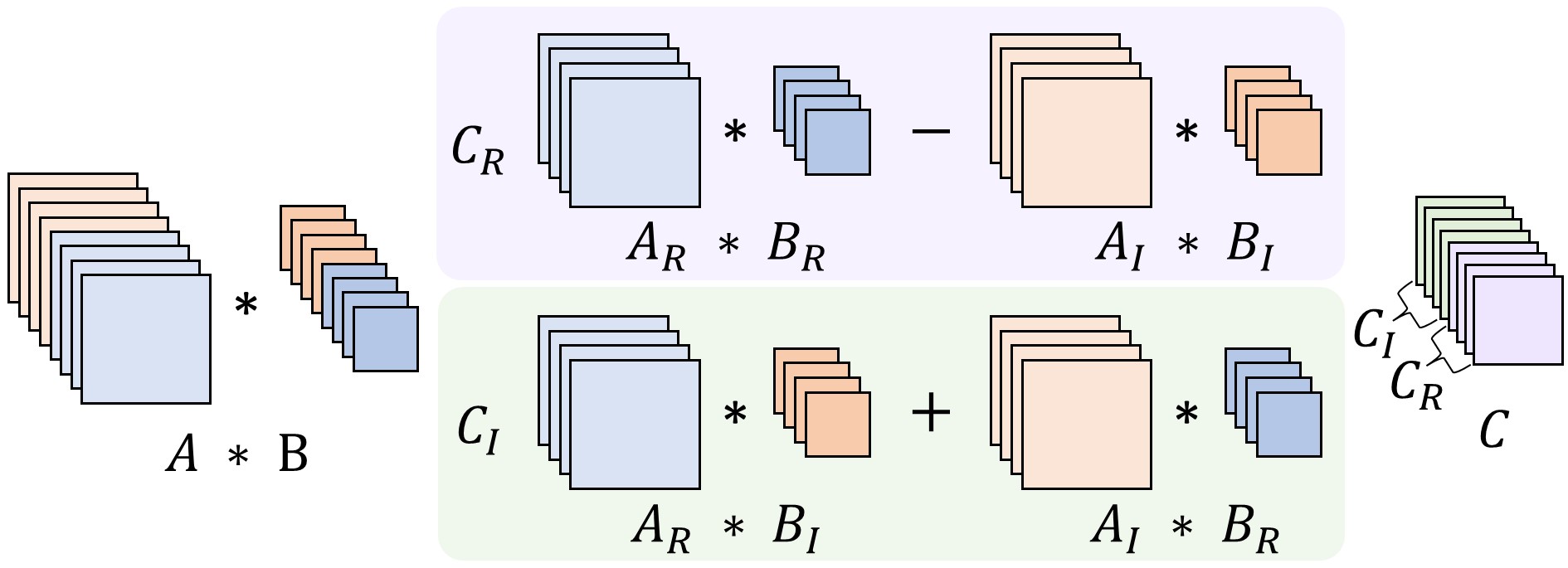
CVNNs deploy complex numbers to both their data and layer operations. To handle data as complex number, CVNNs use complex-valued weights and activations, which are represented in either rectangular or polar form. For the ease of computation in DNN frameworks, CVNNs separately store the real and imaginary parts of complex numbers as two real-valued tensors. In terms of layer operations, CVNNs use complex-valued operations, such as complex-valued convolution, complex-valued fully connected, and complex-valued activation functions. Complex-valued operations basically operate with the same principles as real-valued operations, but with complex numbers. For example, complex-valued convolution is performed by convolving the real and imaginary parts of the input tensor with the real and imaginary parts of the kernel tensor, and then adding the results together [Figure 1].

These capabilities enable CVNNs to model and process complex-valued data more effectively than real-valued neural networks. However, This also introduces significant challenges in terms of complex number representation and operation, both compute and memory intensive. Firstly, complex numbers require twice the memory and computation compared to real numbers. Secondly, complex-valued operations are more complex than real-valued operations, requiring more computation and memory access. Previous studies have shown that CVNNs also achieve higher performance even they reduce the number of parameters by half to compensate for the increased memory and computation requirements. Even with the reduced number of parameters, CVNNs still exhibit higher complexity than real-valued neural networks due to their complex-valued operations.

Polar Form-Aware Quantization (Lee et al., 2023)

Our approach focuses on exploring and leveraging the inherent properties of complex numbers to mitigate the challenges faced by CVNNs. We discovered that by representing complex numbers in their polar form (magnitude and phase), we can exploit their unique value distributions, which differ significantly from the rectangular form (real and imaginary components).

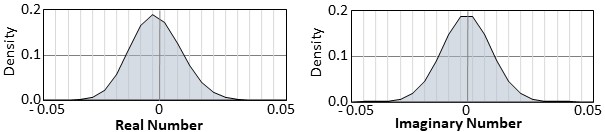
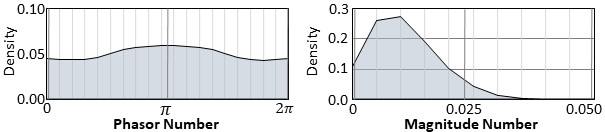
Through our analysis, we found that the polar form presents a more uniform distribution [Figure 2, 3]. Phasor values show a value distribution that has a limited value range, 0 to 2π, and magnitude values show an asymmetric distribution which only has positive values. These limited value ranges and distributions can be exploited in quantization more effectively than the rectangular form, since they can be represented with fewer bits without significant loss of accuracy. This observation led us to develop a Polar Form-Aware Quantization (PAQ) technique, aiming at reducing the memory footprint of CVNNs without significant loss of accuracy.

To fully utilize the advantages offered by the PAQ and effectively accelerate CVNNs, we propose a co-designed hardware accelerator. This accelerator is specifically designed to support PAQ and CVNN operations, alongside a CVNN-aware scheduling scheme that optimizes performance and resource utilization. Our design achieves significant data compression and a performance increase, marking a step forward in the efficient implementation of CVNNs.

For more details on our approach, techniques, and evaluation results, please refer to our publication: “Exploiting Inherent Properties of Complex Numbers for Accelerating Complex Valued Neural Networks.”

We currently have ongoing project on efficient CVNN acceleration, including quantization and hardware design, so if you are interested in our project, please feel free to contact me.